9021. Count the integers of the form 2^x * 3^y
Find the number
of integers in the range [a, b] that can be represented
in the form 2x * 3y where x ≥ 0 and y ≥
0.
Input. Contains no more
than 106 lines. Each line
contains two integers a and b (0 ≤ a ≤ b ≤ 1018), representing a
single query.
Output. For each query,
print on a separate line the number of integers within the range [a, b] inclusive that can be written in the form 2x
* 3y.
|
Sample input |
Sample output |
|
1 10 100 200 |
7 5 |
SOLUTION
binary search
Algorithm analysis
There are not so many numbers of the form 2x * 3y that do not exceed 1018. We can generate
them and store them in an array v.
The number of such values f(a, b)
in the range [a, b] can be found using the formula:
f(0, b) – f(0, a – 1)
Here, f(0, q)
represents the number of values of the form 2x *
3y that do not exceed q. This can be efficiently
found using binary search on the array v.
Example
Let’s generate all numbers of the form 2x * 3y that do not exceed 200.
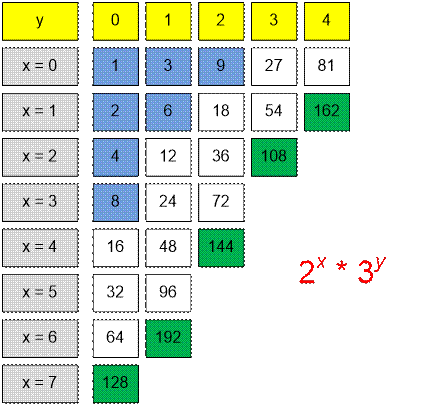
The interval [1; 10] contains 7 numbers
(highlighted in blue).
The interval [100; 200] contains 5 numbers
(highlighted in green).
Let's find the solution for the interval [10; 20]:
upper_bound(v.begin(), v.end(),
20) – upper_bound(v.begin(), v.end(), 9) = 3
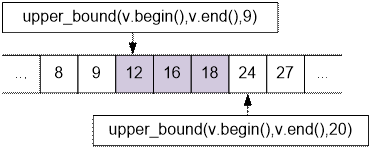
Indeed, the interval [10; 20] contains 3
numbers of the desired form:
12, 16, 18
Algorithm implementation
Let’s define the constant MAX = 1018
and an array v.
#define MAX
1000000000000000000LL
vector<long long>
v;
The function preprocess generates all numbers of the form 2x * 3y that do not exceed 1018 and stores them in the array v. For
each value of x = 1, 2, 4, 8, … iterate over numbers y = 1, 3, 9,
27, … until x * y < MAX.
void preprocess()
{
long long x =
1, y = 1;
while (x
< MAX)
{
while (x *
y < MAX)
{
v.push_back(x
* y);
y *= 3;
}
x *= 2;
y = 1;
}
Sort the
numbers in the array v.
sort(v.begin(), v.end());
}
The main
part of the program. Generate the array of numbers of the form 2x * 3y.
preprocess();
Read a
query – the interval [a, b]. The number of
desired integers in this interval is computed using the formula:
f(a, b) = f(0, b) – f(0, a – 1)
while (scanf("%lld
%lld", &a, &b) == 2)
{
res =
upper_bound(v.begin(), v.end(), b) –
upper_bound(v.begin(), v.end(), a - 1);
printf("%lld\n", res);
}